Simultaneous Linear Equations
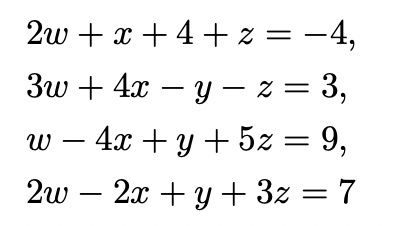
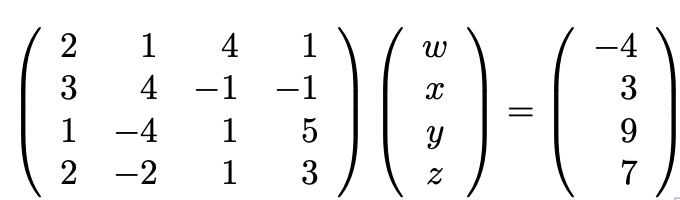
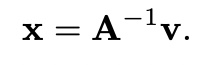
- Guass-Jorda Elimination
- Backsubstitution
- Pivoting
- LU Decomposition
- Inverse of a Matrix
- Tridagonal and banded Matrices
Eigenvalues and Eigenvectors
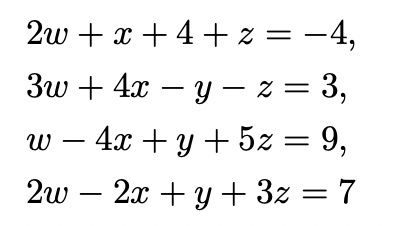
with matrix form,
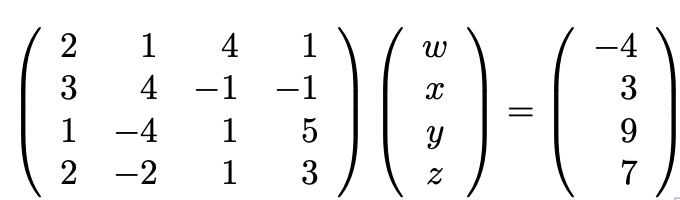
represent with Matrix A, and vector x, v
achive sol by inverse matrix
Gauss-Jordan Elimination
rules for Gauss-Jordan Elimination
1. if we multiply any row of the matrix A by any constant,
and we multiply the correponding row of the vector v by the same constant,
then the solution does not change.
2. if we add to or substract from any row of A a mltiple of any other row, and we do the
same for the vector v, then the solutio ndoes not change.
after Gauss-Jordan Elimination achive "Upper Diagonal Matrix”
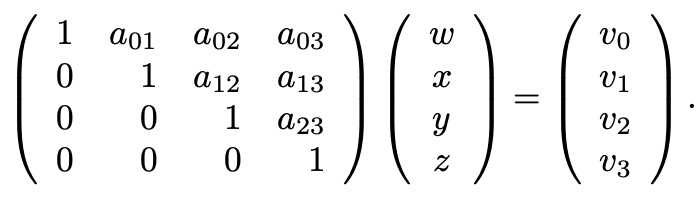
Backsubstitution
can be written as,
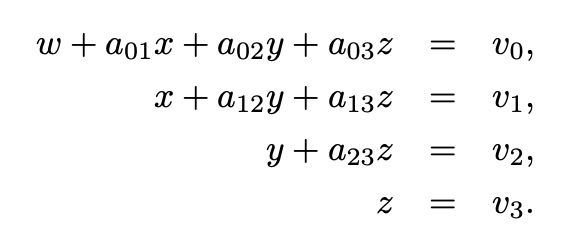
x_i=v_i-sigma( {j=i+1}^{n-1}(a_ij*x_j) ) <- x_i는 역순으로 구해야 함
# Gaussian-Jordan Elimination
from numpy as np
A=np.array([[2, 1, 4, 1], [3, 4, -1, -1], [1, -4, 1, 5], [2, -2, 1, 3]], float)
v=np.array([-4, 3, 9, 7], float)
N=A.shape[0]; M=A.shape[1]
x=np.zeros([4, 1], float)
for n in range(N): # build Upper Triangle Matrix(U)
div=A[n, n]
A[n, :]/=div # make A[n, n]==1
v[n]/=div
for i in range(n+1, N): # make A[n, :n]==0
mult=A[i, n]
A[i, :]-=mult*A[n, :]
v[i]-=mult*v[n]
# Backsubstitution
for i in range(N-1, -1, -1):
x[i]=v[i]
for j in range(i+1, N):
x[i]-=A[i, j]*x[j]
print("solution x=\n", x, sep="")
Pivoting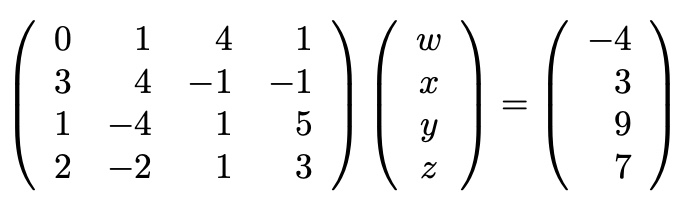
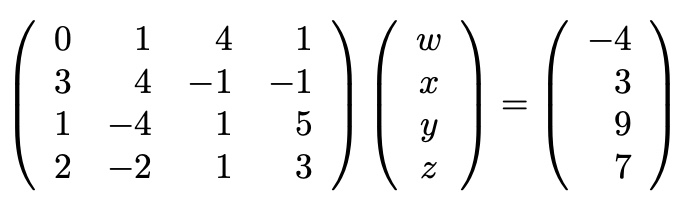
first element가 zero인 경우(Divide by zero is not allowed)
일반적으로 0과 가장 거리가 먼 행과 변경
Partial Pivoting
# Gaussian-Jordan Elimination
import numpy as np
A=np.array([[0, 1, 4, 1], [3, 4, -1, -1], [1, -4, 1, 5], [2, -2, 1, 3]], float)
v=np.array([-4, 3, 9, 7], float)
N=A.shape[0]; M=A.shape[1]
x=np.zeros([4, 1], float)
for n in range(N):
# Partial Pivoting
max_el=abs(A[n, n])
loc_max_el=n
for j in range(n+1, N):
if abs(A[j, n])>max_el:
max_el=abs(A[j, n])
loc_max_el=j
if loc_max_el!=n:
A_tmp=A[n, :].copy()
A[n, :]=A[loc_max_el, :]
A[loc_max_el, :]=A_tmp
v_tmp=v[n].copy()
v[n]=v[loc_max_el]
v[loc_max_el]=v_tmp
###
div=A[n, n]
A[n, :]/=div
v[n]/=div
for i in range(n+1, N):
mult=A[i, n]
A[i, :]-=mult*A[n, :]
v[i]-=mult*v[n]
# Backsubstitution
for i in range(N-1, -1, -1):
x[i]=v[i]
for j in range(i+1, N):
x[i]-=A[i, j]*x[j]
print("solution x=\n", x, sep="")
Gauss-Jordan Elimination in Matrix Form
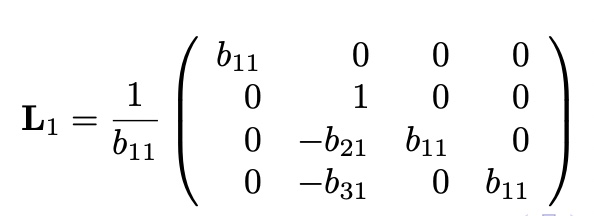
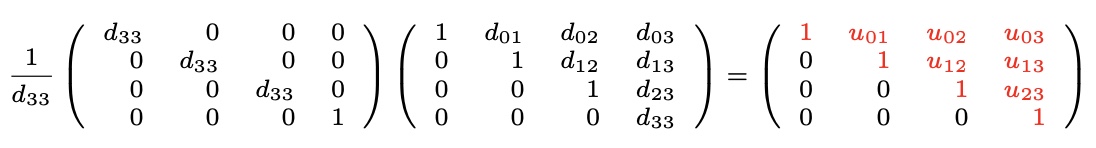
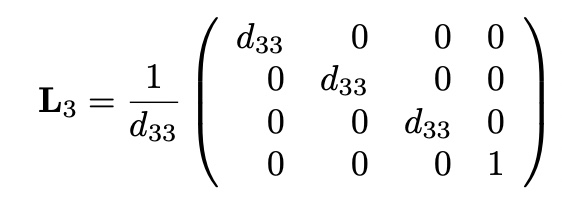
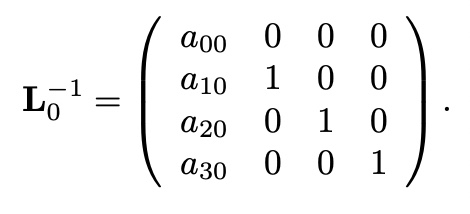
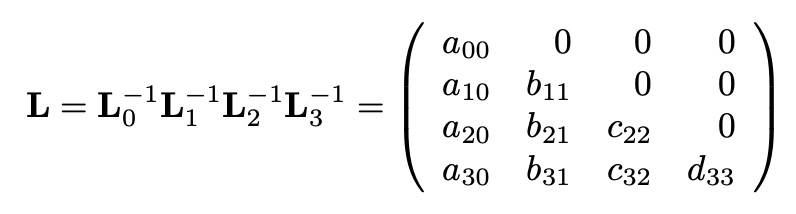
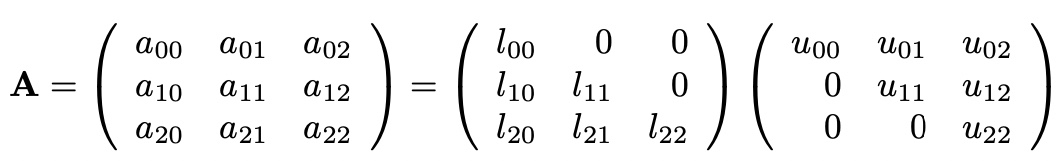
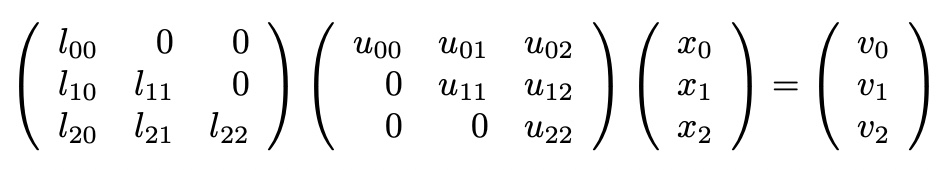
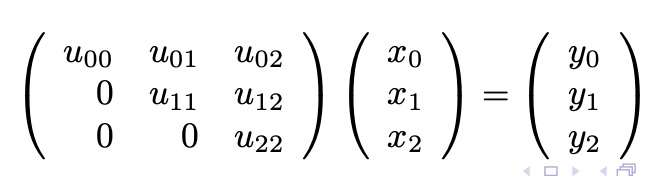with y,
, 
, 
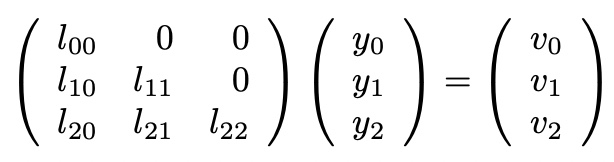
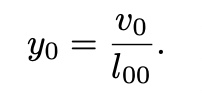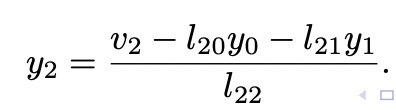
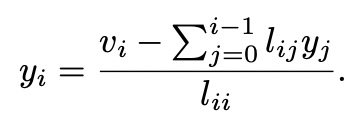
Repeating Gauss-Jordan elimination would be time-consuming(역행렬 연산에서 연산량 큼)
step 1:
Define lower triangular matrix L_0 as,
step 2:
Define lower trianuglar matrix L_1 as,
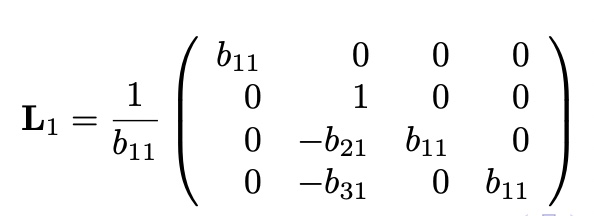
step 3:
Define lower trianuglar matrix L_2 as,
step 4:
=
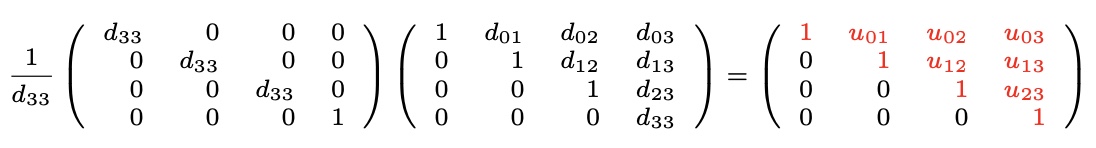
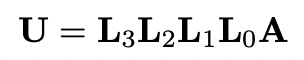
Define lower trianuglar matrix L_3 as,
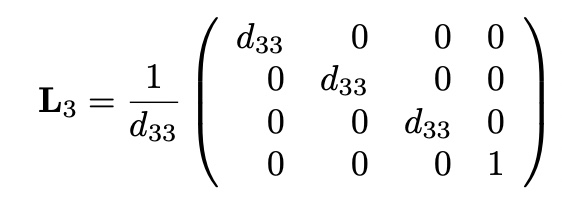
Dfine two matrices:
(L is Lower triangular matrix, U is Upper triangle matrix)
then,
from A^-1.dot(A)= I (Identity)
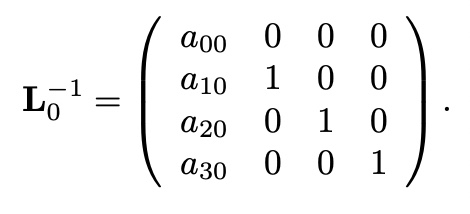
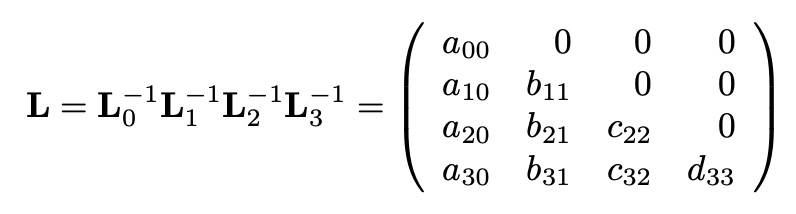
LU Decomposition-Backsubtraction
express with 3x3 matrix A
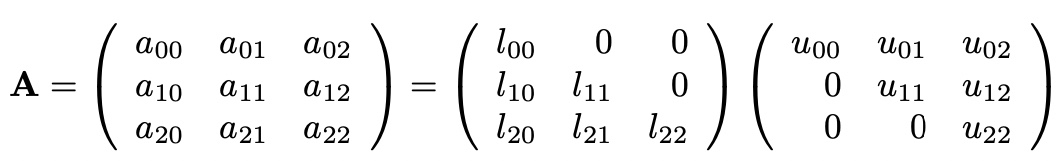
with Ax=v
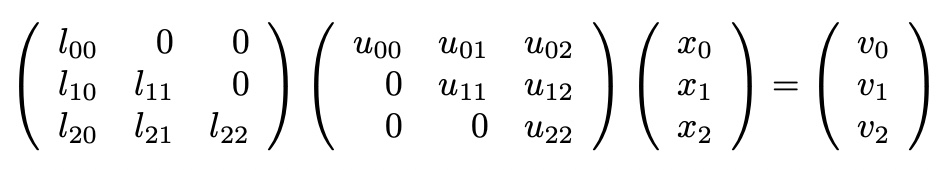
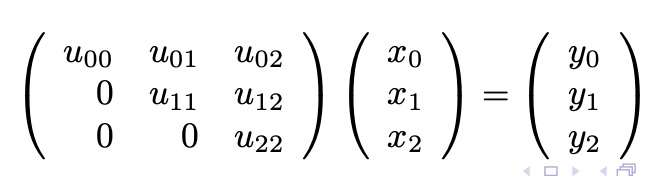with y,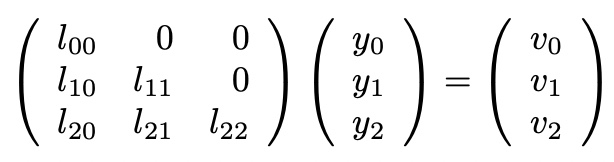y satisfied,
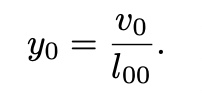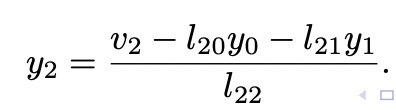
, , then,
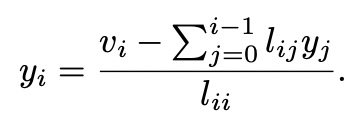
매 단계마다 Paritial Pivoting 필요
from numpy.linalg import solve
x=solve(A, v) # 역행렬 곱해서 연산
LU decomposition with partial pivoting
# Gaussian-Jordan Elimination
import numpy as np
A=np.array([[0, 1, 4, 1], [3, 4, -1, -1], [1, -4, 1, 5], [2, -2, 1, 3]], float)
v=np.array([-4, 3, 9, 7], float)
N=A.shape[0]; M=A.shape[1]
x=np.zeros([N, 1], float)
L=np.zeros_like(A)
U=np.copy(A)
for n in range(N):
# Partial Pivoting
max_el=abs(U[n, n])
loc_max_el=n
for j in range(n+1, N):
if abs(U[j, n])>max_el:
max_el=abs(U[j, n])
loc_max_el=j
if loc_max_el!=n:
U_tmp=U[n, :].copy()
U[n, :]=U[loc_max_el, :]
U[loc_max_el, :]=U_tmp
L_tmp=L[n, :].copy()
L[n, :]=L[loc_max_el, :]
L[loc_max_el, :]=L_tmp
A_tmp=A[n].copy()
A[n]=A[loc_max_el]
A[loc_max_el]=A_tmp
v[n], v[loc_max_el]=v[loc_max_el], v[n]
###
L[n:, n]=U[n:, n]
# divide by the diagonal element
div=U[n, n]
U[n, :]/=div
for i in range(n+1, N):
mult=U[i, n]
U[i, :]-=mult*U[n, :]
print("A=", A)
print("LU=", np.dot(L, U))
# Backsubstitution
y=np.zeros_like(v, float)
for i in range(M):
y[i]=v[i]
for j in range(0, i):
y[i]-=L[i, j]*y[j]
y[i]/=L[i, i]
for i in range(M-1, -1, -1):
x[i]=y[i]
for j in range(i+1, M):
x[i]-=U[i, j]*x[j]
#x[i]/=U[i, i]
print("solution x=\n", x, sep="")
Calculating the Inverse of a Matrix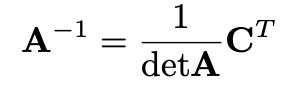
seperate with column
n 번의 Gauss-Jordan elimination or LU decompositon을 이용해서 해를 구할 수 있음
V=I로 둘경우, X가 A의 inverse matrix가 됨
from numpy.linalg import inv
X=inv(A)
Inverse Matrix
# Gaussian-Jordan Elimination
import numpy as np
A=np.array([[0, 1, 4, 1], [3, 4, -1, -1], [1, -4, 1, 5], [2, -2, 1, 3]], float)
N=A.shape[0]; M=A.shape[1]
L=np.zeros_like(A)
U=np.copy(A)
V=np.diag([1, 1, 1, 1])
for n in range(N):
# Partial Pivoting
max_el=abs(U[n, n])
loc_max_el=n
for j in range(n+1, N):
if abs(U[j, n])>max_el:
max_el=abs(U[j, n])
loc_max_el=j
if loc_max_el!=n:
U_tmp=U[n, :].copy()
U[n, :]=U[loc_max_el, :]
U[loc_max_el, :]=U_tmp
L_tmp=L[n, :].copy()
L[n, :]=L[loc_max_el, :]
L[loc_max_el, :]=L_tmp
#A_tmp=A[n].copy()
#A[n]=A[loc_max_el]
#A[loc_max_el]=A_tmp
V_tmp=V[n, :].copy()
V[n, :]=V[loc_max_el, :]
V[loc_max_el, :]=V_tmp
###
L[n:, n]=U[n:, n]
# divide by the diagonal element
div=U[n, n]
U[n, :]/=div
for i in range(n+1, N):
mult=U[i, n]
U[i, :]-=mult*U[n, :]
print("LU=", np.dot(L, U))
# Backsubstitution
Y=np.zeros_like(V, float)
X=np.zeros_like(V, float)
for i in range(N):
for j in range(N):
Y[j, i]=V[j, i]
for k in range(j):
Y[j, i]-=L[j, k]*Y[k, i]
Y[j, i]/=L[j, j]
for i in range(N):
for j in range(N-1, -1, -1):
X[j, i]=Y[j, i]
for k in range(j+1, N):
X[j, i]-=U[j, k]*X[k, i]
X[j, i]/=U[j, j]
print("X=", X)
#A=np.array([[0, 1, 4, 1], [3, 4, -1, -1], [1, -4, 1, 5], [2, -2, 1, 3]], float)
print("I=", A.dot(X))
Tridiagonal Matrices: Trigonal Matrix Algorithm or Thomas Algorithm
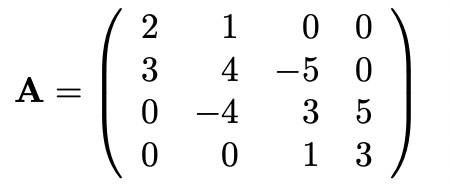
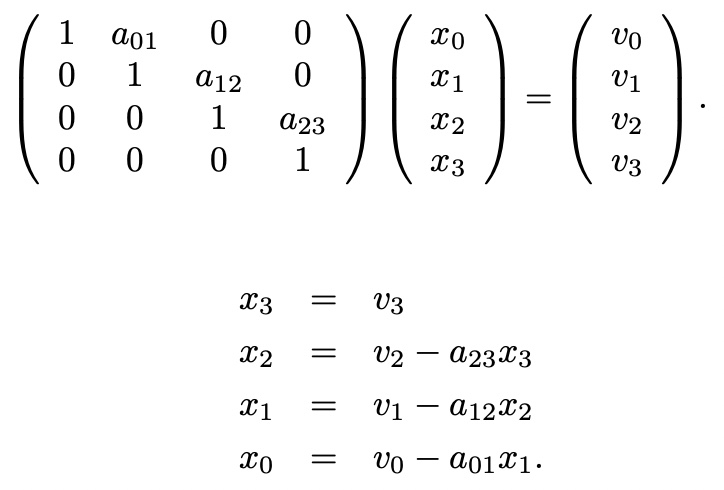
Matrix has nonzero elements only along the diagonal and immediately above and below it
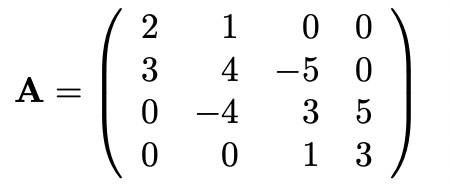
with Gauss Jordan Elimination(make Trigonal Matrix)
Backsubstitution
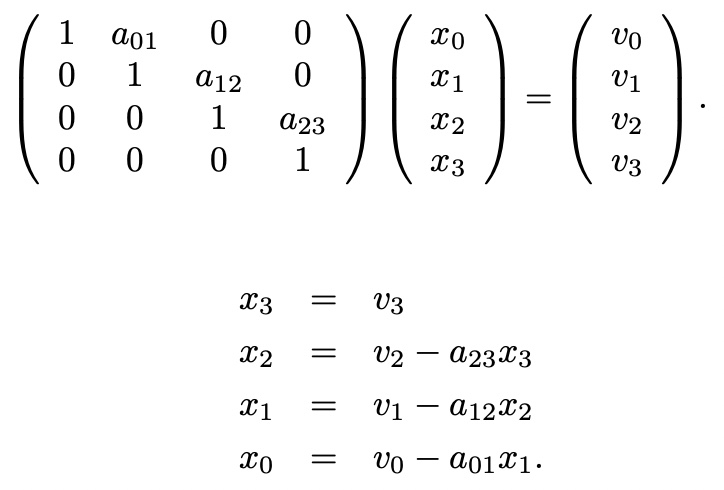
Banded Matrix
triangular Matrix는 더 간단하게 Gauss Jordan Elimination 가능
Vibration in a One-Dimensional System
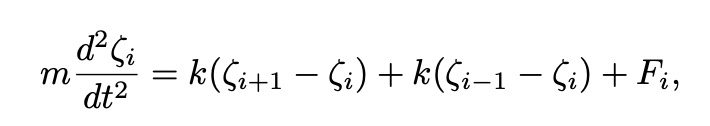
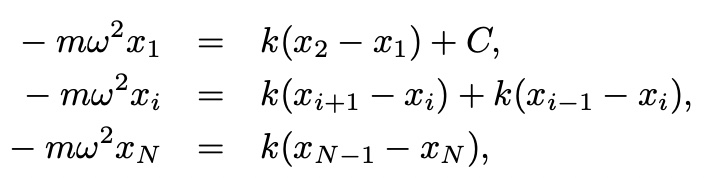
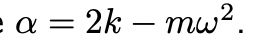
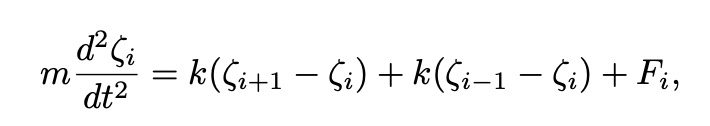
The masses at the two end
assuming,
and
then,
->
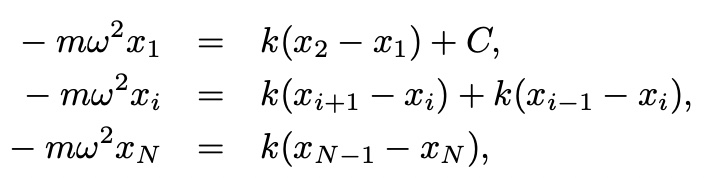
with
set m=1, k=6, w=2
# Vibration in a One-Dimensional System1
import numpy as np
import matplotlib.pyplot as plt
N=26
C=1.0
m=1.0
k=6.0
omega=2.0
alpha=2*k-m*omega**2
# Build trigonal
A=np.zeros([N, N])
for i in range(N-1):
A[i, i]=alpha
A[i, i+1]=-k
A[i+1, i]=-k
A[0, 0]-=k
A[N-1, N-1]=alpha-k
v=np.zeros(N, float)
v[0]=C
# xx=np.linalg.solve(A, v)
for i in range(N-1):
div=A[i, i]
A[i, i]/=div
A[i, i+1]/=div
v[i]/=div
if i==N-2:
n=2
else:
n=3
a_tmp=A[i+1, i]
for j in range(n):
A[i+1, i+j]-=A[i, i+j]*a_tmp
v[i+1]-=a_tmp*v[i]
A[i+1, i]=0
v[N-1]/=A[N-1, N-1]
A[N-1, N-1]/=A[N-1, N-1]
# backsubstitution
x=np.zeros_like(v, float)
x[N-1]=v[N-1]
for i in range(N-2, -1, -1):
x[i]=v[i]-A[i, i+1]*x[i+1]
plt.plot(x)
plt.plot(x, "ko", ms=15.0)
plt.plot(xx, "rs")
plt.show()
more optimized(Teoplitz-Trigonal matrix only)
import numpy as np
import matplotlib.pyplot as plt
N=26
C=1.0
m=1.0
k=6.0
omega=2.0
alpha=2*k-m*omega**2
# Build trigonal
A=np.zeros([N, N])
for i in range(N-1):
A[i, i]=alpha
A[i, i+1]=-k
A[i+1, i]=-k
A[0, 0]-=k
A[N-1, N-1]=alpha-k
###
v=np.zeros(N, float)
v[0]=C
# xx=np.linalg.solve(A, v)
for i in range(N-1):
div=A[i, i]
A[i, i]/=div
A[i, i+1]/=div
v[i]/=div
mul=A[i+1, i]
A[i+1, i+1]-=mul*A[i, i+1]
v[i+1]-=mul*v[i]
A[i+1, i]=0
v[N-1]/=A[N-1, N-1]
A[N-1, N-1]/=A[N-1, N-1]
# backsubstitution
x=np.zeros_like(v, float)
x[N-1]=v[N-1]
for i in range(N-2, -1, -1):
x[i]=v[i]-A[i, i+1]*x[i+1]
plt.plot(x)
plt.plot(x, "ko", ms=15.0)
plt.plot(xx, "rs")
plt.show()
Eigenvalues and Eigenvectors
in physics
- Mechanics
- Electromagnetism
- Quantum mechanism
- etc.
only focus on real Symmetric matrix A
for Symmetric matrix A’s eigenvectors are orthogonal
QR decomposition to eigenvectors, eigenvalues
from eigen decomposition
because V is Orthogonal matrix
rewrite the matrix A as product QR
Q: an orthogonal matrix, R: Upper-triangular matrix
and define
then,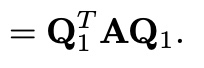 
set,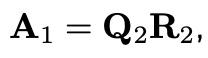 
then,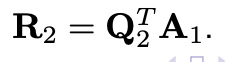 
and define
Repeat the process up to total k steps then,
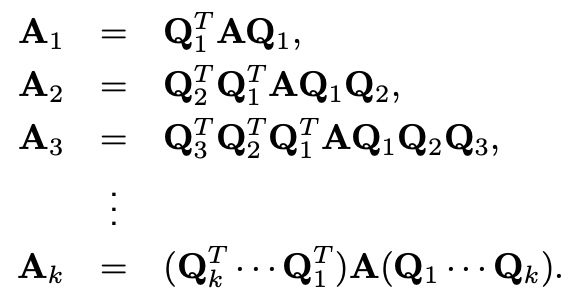
process long enough, matrix A_k become diagonal.
set,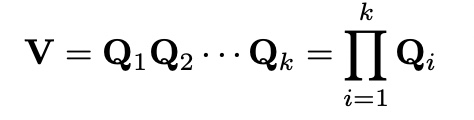 
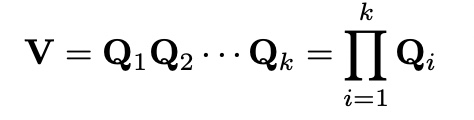
same as eigen decomposition
QR decomposition
1. Create NxN matrix V to hold the eigenvectors
2. Initialize V to be equal to the identity matrix I
3. Choose a target accuracy for off-diagonal elements of the eigenvalue matrix
4. Calculate the QR decomposition A=QR
5. Update A to the new value A=RQ
6. Multiply V on the right by Q
7. Check the off-diagonal elemetns of A. If they are all less than error, we are done
otherwise go back to step 4
import numpy as np
V=np.linalg.eigh(A)
lamb=np.linalg.eigvalsh(A)
then, how to QR decomposition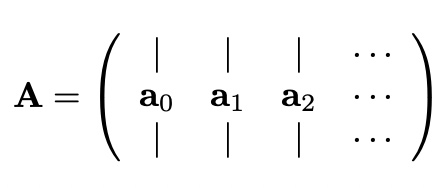
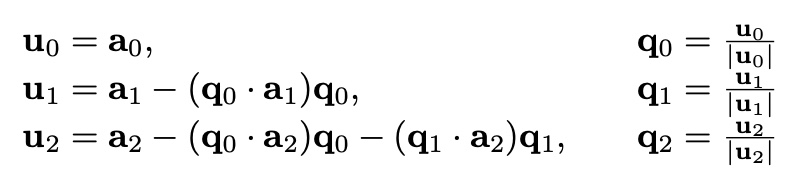
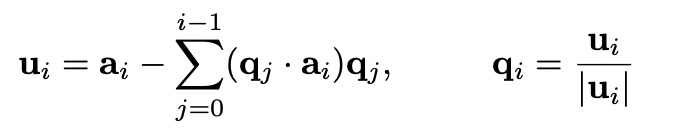
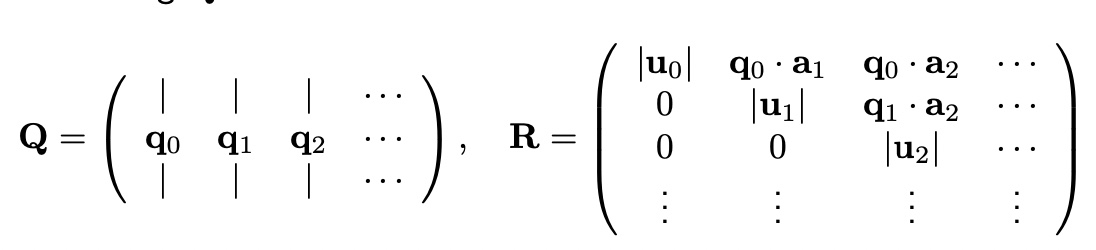
with A
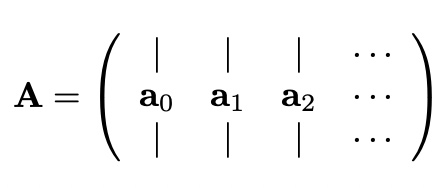
Gram-Schmidt Orthogonalization
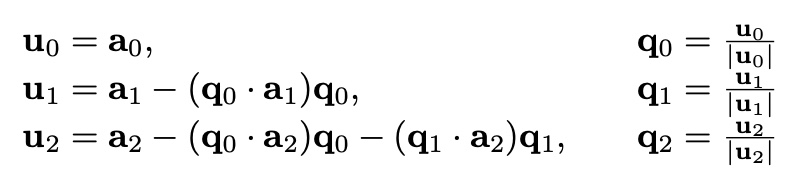
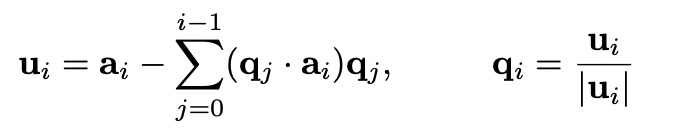
then,
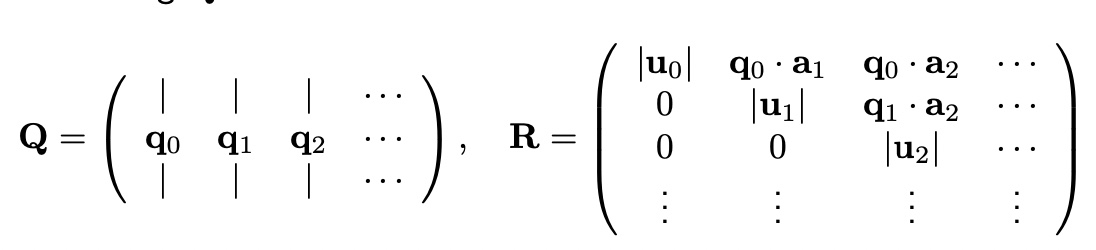
eigenvectors & eigenvalues
import numpy as np
A=np.array([[1, 4, 8, 4], [4, 2, 3, 7], [8, 3, 6, 9], [4, 7, 9, 2]], float)
xx, VV=np.linalg.eigh(A)
N=A.shape[1]
U=np.zeros_like(A, float)
Q=np.zeros_like(A, float)
R=np.zeros_like(A, float)
# Initialize V
diag=np.ones(N, float)
V=np.diag(diag)
delta=1.0
epsilon=1.e-10
while delta>epsilon:
# QR decomposition(Q)
for i in range(N):
U[:, i]=A[:, i]
if i>0:
for j in range(i):
U[:, i]-=(np.dot(Q[:, j], A[:, i])*Q[:, j])
magU=np.dot(U[:, i], U[:, i])**(1/2)
Q[:, i]=U[:, i]/magU
# QR decomposition(R)
for j in range(N):
for k in range(N):
if j>k:
R[j, k]=0
elif j==k:
R[j, k]=np.dot(U[:, j], U[:, j])**(1/2)
else:
R[j, k]=np.dot(Q[:, j], A[:, k])
###
# solve eigenvectors & eigenvalues
A=np.dot(R, Q)
V=np.dot(V, Q)
delta=0.0
for j in range(N):
for k in range(N):
if j<k:
if delta<abs(A[j, k]):
delta=abs(A[j, k])
lamb=np.zeros(N, float)
for i in range(N):
lamb[i]=A[i][i]
# lamb is eigenvals
# V is eigenvectros